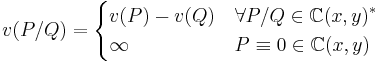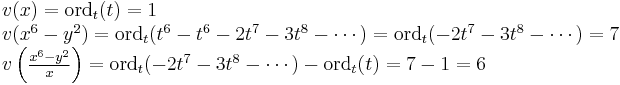Valuation (algebra)
In algebra (in particular in algebraic geometry or algebraic number theory), a valuation is a function on a field that provides a measure of size or multiplicity of elements of the field. They generalize to commutative algebra the notion of size inherent in consideration of the degree of a pole or multiplicity of a zero in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic or analytic varieties in algebraic geometry. A field with a valuation on it is called a valued field.
Contents |
Definition
To define the algebraic concept of valuation, the following objects are needed:
- a field K and its multiplicative subgroup K×,
- an abelian totally ordered group (Γ, +, ≥) (which could also be given in multiplicative notation as (Γ, ·, ≥)).
The ordering and group law on Γ are extended to the set Γ∪{∞}[1] by the rules
- ∞ ≥ α for all α in Γ,
- ∞ + α = α + ∞ = ∞ for all α in Γ.
Then a valuation of K is any map
- v : K → Γ∪{∞}
which satisfies the following properties for all a, b in K:
- v(a) = ∞ if, and only if, a = 0,
- v(ab) = v(a) + v(b),
- v(a + b) ≥ min(v(a), v(b)).
Some authors use the term exponential valuation rather than "valuation". In this case the term "valuation" means "absolute value".
A valuation v is called trivial (or the trivial valuation of K) if v(a) = 0 for all a in K×, otherwise it is called non-trivial.
For valuations used in geometric applications, the first property implies that any non-empty germ of an analytic variety near a point contains that point. The second property asserts that any valuation is a group homomorphism, while the third property is a translation of the triangle inequality from metric spaces to ordered groups.
It is possible to give a dual definition of the same concept using the multiplicative notation for Γ: if, instead of ∞, an element O[2] is given and the ordering and group law on Γ are extended by the rules
- O ≤ α for all α in Γ,
- O · α = α · O = O for all α in Γ,
then a valuation of K is any map
- v : K → Γ∪{O}
satisfying the following properties for all a, b in K:
- v(a) = O if, and only if, a = 0,
- v(ab) = v(a) · v(b),
- v(a + b) ≤ max(v(a), v(b)).
(Note that in this definition, the directions of the inequalities are reversed.)
A valuation is commonly assumed to be surjective, since many arguments used in ordinary mathematical research involving those objects use preimages of unspecified elements of the ordered group contained in its codomain. Also, the first definition of valuation given is more frequently encountered in ordinary mathematical research, thus it is the only one used in the following considerations and examples.
Associated objects
If v : K → Γ∪{∞} is a valuation, then there are several objects that can be defined from it:
- the value group of v (or valuation group of v), denoted Γv, is v(K×), it is a subgroup of Γ,
- the valuation ring of v, denoted Rv is the set of elements a of K such that v(a) ≥ 0, it is a valuation ring,
- the prime ideal of v (or the maximal ideal of v), denoted mv is the set of elements a of K such that v(a) > 0, it is a maximal ideal of Rv,
- the residue field of v, denoted kv is Rv/mv, it is a field.
Basic properties
Equivalence of valuations
Two valuations v1 and v2 of K with valuation group Γ1 and Γ2, respectively, are said to be equivalent if they have there is an order-preserving group isomorphism φ : Γ1 → Γ2 such that v2(a) = φ(v1(a)) for all a in K×. This is an equivalence relation.
Two valuations of K are equivalent if, and only if, they have the same valuation ring.
An equivalence class of valuations of a field is called a place. Ostrowski's theorem gives a complete classification of places of the field of rational numbers Q: these are precisely the equivalence classes of valuations for the p-adic completions of Q.
Extension of valuations
Let v be a valuation of K and let L be a field extension of K. An extension of v (to L) is a valuation w of L such that the restriction of w to K is v. The set of all such extensions is studied in the ramification theory of valuations.
Let L/K be a finite extension and let w be an extension of v to L. The index of Γv in Γw, e(w/v) = [Γw : Γv], is called the reduced ramification index of w over v. It satisfies e(w/v) ≤ [L : K] (the degree of the extension L/K). The relative degree of w over v is defined to be f(w/v) = [Rw/mw : Rv/mv] (the degree of the extension of residue fields). It is also less than or equal to the degree of L/K. When L/K is separable, the ramification index of w over v is defined to be e(w/v)pi, where pi is the inseparable degree of the extension Rw/mw over Rv/mv.
Complete valued fields
When the ordered abelian group Γ is the additive group of the integers, the associated absolute value induces a metric on the field K. If K is complete with respect to this metric, then it is called complete valued field.
Examples
π-adic valuation
Let R be a principal ideal domain, K be its field of fractions, and π be an irreducible element of R. Since every principal ideal domain is a unique factorization domain, every non-zero element a of R can be written (essentially) uniquely as
where the e's are non-negative integers and the pi are irreducible elements of R that are not associates of π. In particular, the integer ea is uniquely determined by a.
The π-adic valuation of K is then given by
If π' is another irreducible element of R such that (π') = (π) (that is, they generate the same ideal in R), then the π-adic valuation and the π'-adic valuation are equal. Thus, the π-adic valuation can be called the P-adic valuation, where P = (π).
When R is the ring of integers Z, then K is the rational numbers Q, and π is some prime number p (or its negative). The π-adic valuation obtained is the p-adic valuation on Q.
P-adic valuation on a Dedekind domain
The previous example can be generalized to Dedekind domains. Let R be a Dedekind domain, K its field of fractions, and let P be a non-zero prime ideal of R. Then, the localization of R at P, denoted RP, is a principal ideal domain whose field of fractions is K. The construction of the previous section applied to the prime ideal PRP of RP yields the P-adic valuation of K.
Geometric notion of contact
Let ![\scriptstyle\mathfrak{{R}} = \mathbb{{C}}[x,y]](/2012-wikipedia_en_all_nopic_01_2012/I/f50178df7776027c739fdbddb1c8a8f3.png) be the ring of polynomials of two variables over the complex field,
be the ring of polynomials of two variables over the complex field, 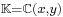 be the field of rational functions over the same field, and consider the (convergent) power series
be the field of rational functions over the same field, and consider the (convergent) power series
whose zero set, the analytic variety 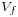 , can be parametrized by one coordinate
, can be parametrized by one coordinate  as follows
as follows
It is possible to define a map ![\scriptstyle v: \mathbb{{C}}[x,y] \rightarrow \mathbb{Z}](/2012-wikipedia_en_all_nopic_01_2012/I/714432c41dd93d43dd6ee533a0dc757e.png) as the value of the order of the formal power series in the variable
as the value of the order of the formal power series in the variable  obtained by restriction of any polynomial
obtained by restriction of any polynomial  in
in ![\scriptstyle\mathbb{C}[x,y]](/2012-wikipedia_en_all_nopic_01_2012/I/ce43d1657b0bf627d3fc36798cdc3521.png) to the points of the set
to the points of the set 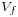
It is also possible to extend the map  from its original ring of definition to the whole field
from its original ring of definition to the whole field 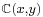 as follows
as follows
As the power series  is not a polynomial, it is easy to prove that the extended map
is not a polynomial, it is easy to prove that the extended map  is a valuation: the value
is a valuation: the value 
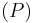 is called intersection number between the curves (1-dimensional analytic varieties)
is called intersection number between the curves (1-dimensional analytic varieties) 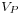 and
and 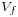 . As an example, the computation of some intersection numbers follows
. As an example, the computation of some intersection numbers follows
See also
Notes
- ^ The symbol ∞ denotes an element not in Γ, and has not any other meaning. His properties are simply defined by axioms, as in every formal presentation of a mathematical theory.
- ^ As for the symbol ∞, O denotes an element not in Γ and has not any other meaning, his properties being again defined by axioms.
References
- Jacobson, Nathan (1989) [1980], "Valuations: paragraph 6 of chapter 9", Basic algebra II (2nd ed.), New York: W. H. Freeman and Company, ISBN 0-7167-1933-9, Zbl 0694.16001. A masterpiece on algebra written by one of the leading contributors.
- Chapter VI of Zariski, Oscar; Samuel, Pierre (1976) [1960], Commutative algebra, Volume II, Graduate Texts in Mathematics, 29, New York, Heidelberg: Springer-Verlag, ISBN 978-0-387-90171-8
External links
- Danilov, V.I. (2001), "Valuation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=V/v096010
- Discrete valuation at PlanetMath.
- Valuation at PlanetMath.
- Weisstein, Eric W., "Valuation" from MathWorld.
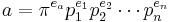
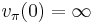
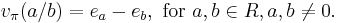
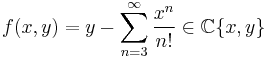
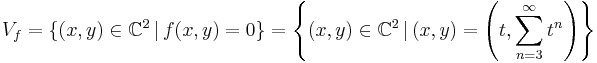
![v(P) = \mathrm{ord}_t\left(P|_{V_f}\right) = {\mathrm{ord}}_t \left(P\left(t,\sum_{n=3}^{%2B\infty}t^n\right)\right) \quad \forall P\in \mathbb{C}[x,y]](/2012-wikipedia_en_all_nopic_01_2012/I/033cef33c2dfbe0105a94ca8d863db40.png)